
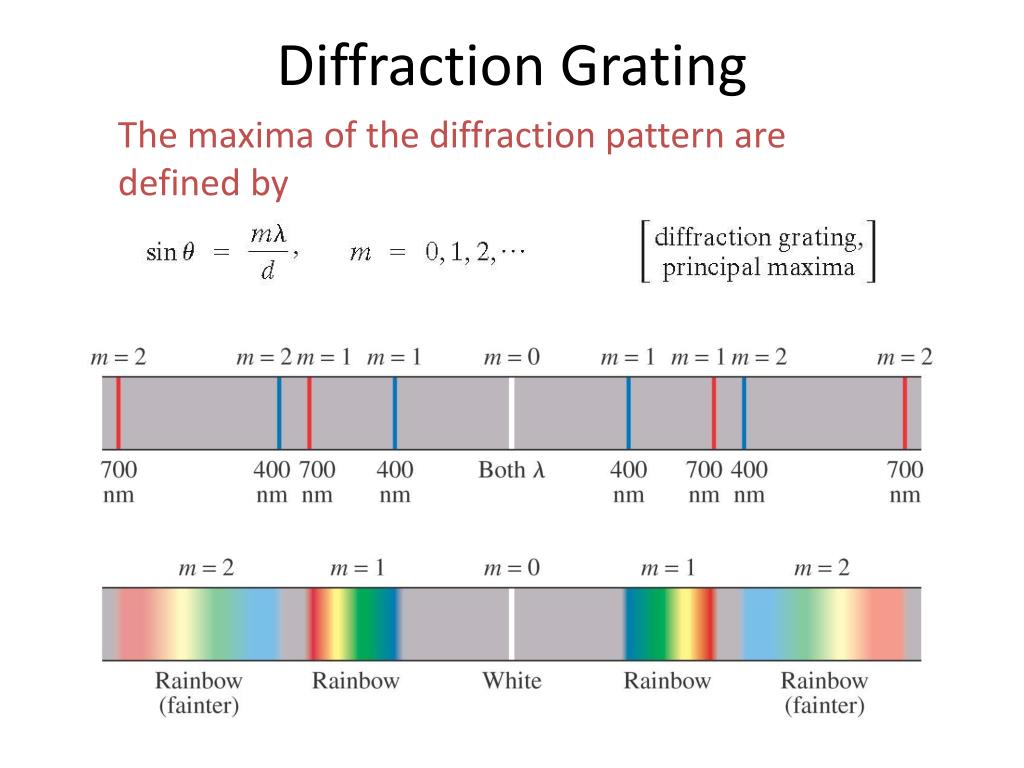
A diffraction pattern is produced only if the wavelength of light λ is comparable to or larger than the size of the obstacle around which it will flow. While the two conditions must be fulfilled to ensure that the phenomenon is observable, there exists another condition which, if not fulfilled, prevents the phenomenon from occurring in the first place. These conditions also must be fulfilled to conspicuously demonstrate diffraction. When the sources are incoherent or multi-chromatic - or worse, both (which is the case with white light) - the bands produced are indistinguishably muddled and not as uniform and distinct. While light does experience interference, it is only conspicuous when the two sources of light are both monochromatic - emitting light of a single wavelength - and coherent - emitting identical waves of a constant phase difference. However, before we can understand how the slit diffracts the light, let’s make one thing clear. The pattern produced by a diffracted laser. The addition causes the luminosity of the region to double, whereas the negation renders the region utterly dark. Young immediately realized that when the two waves are squeezed between the slits, a bright band is produced when the peak of one ripple interferes constructively with or is added to the peak of another ripple, while a dark band is produced when the peak of a ripple interferes destructively with or negates another ripple. Only waves interfering with each other can form such a pattern. The discovery vindicated Huygens, as light cannot bend or flow around an obstacle unless it obeys his principle.
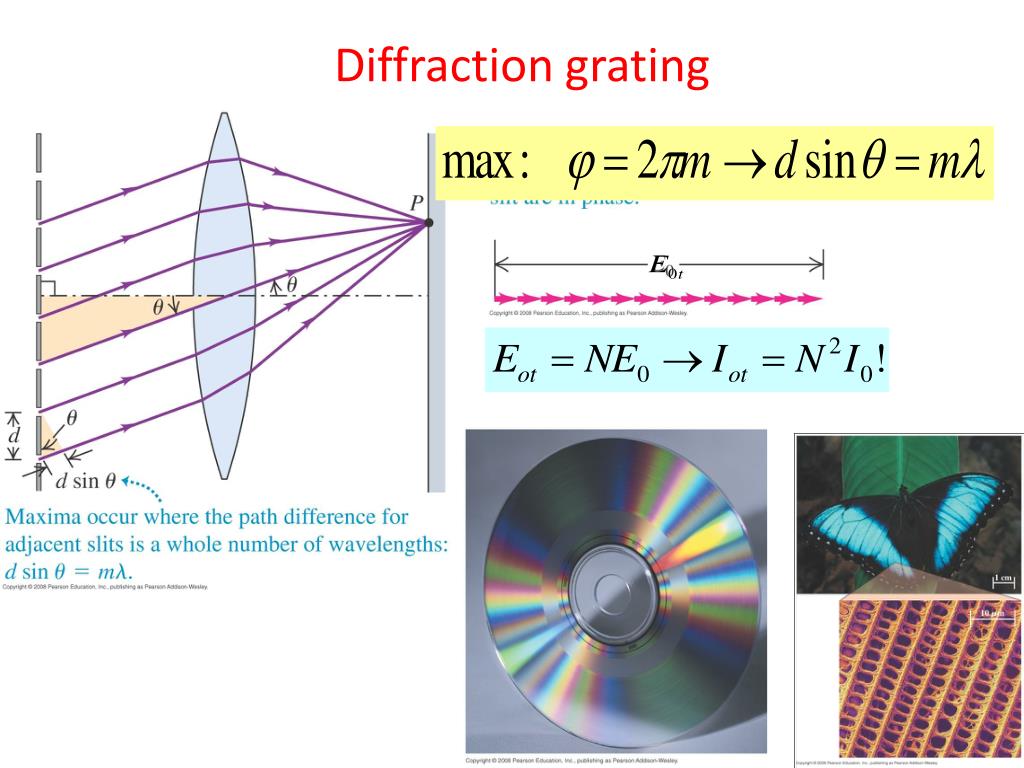
What the squeezed lights illuminated on a screen ahead of them is now called an interference pattern – a uniform, alternating pattern of bright and dark bands. STP diffraction gratings are expected to find exotic practical applications in communication systems, especially for the realization of enhanced-efficiency or full-duplex beam coders, nonreciprocal beam splitters, nonreciprocal and enhanced-resolution holograms, and illusion cloaks.Reflection according to Huygens’ principle.Ī century later, it was the British polymath Thomas Young who successfully demonstrated how light behaves like ripples in a pond by forcing light to squeeze through two adjacent slits. Finally, as a particular example of a practical application of the STP diffraction gratings to communication systems, we propose an original multiple-access communication system featuring full-duplex operation. Additionally, we provide the conditions for Bragg and Raman-Nath diffraction regimes for STP gratings. Furthermore, the theoretical analysis of the structure is supported by time- and frequency-domain finite-difference time-domain (FDTD) numerical simulations for both transmissive and reflective STP diffraction gratings. The theory of the wave diffraction by STP gratings is formulated through satisfying the conservation of both momentum and energy, as well as rigorous Floquet mode analysis. Such spatiotemporally periodic gratings are endowed with enhanced functionalities and exotic characteristics, such as an asymmetric diffraction pattern, nonreciprocal and asymmetric transmission and reflection, and an enhanced diffraction efficiency. We show that, in contrast with conventional spatially periodic gratings, a STP diffraction grating produces spatial diffraction orders, each of which is formed by an infinite set of temporal diffraction orders. This paper studies the theory and applications of the diffraction of electromagnetic waves by space-time-periodic (STP) diffraction gratings.


 0 kommentar(er)
0 kommentar(er)
